Multiple star systems are not the majority in the Universe, even if in our Galaxy only 30 percent of stars are single, like our Sun. Massive stars tend to be more “family-oriented” than low-mass stars. For example, only 15 to 25 percent of M class stars are in binary or multiple systems comparing to 2/3 of G class stars, and G class makes only 7 percent of stars we see. The reason high-mass stars are often in multiples while low-mass ones are not is due to differences in how they form.
Star formation usually occurs in dense turbulent clouds of molecular Hydrogen. The natal environment influences star formation through the complex interplay of gravity, magnetic fields, and supersonic turbulence. Observations suggest that massive stars form through disk accretion in direct analogy to the formation of low-mass stars. However, several aspects distinguish high and low-mass star formation despite the broad similarity of the observed outflow and ejection phenomena.
Surprisingly, the nearby Taurus-Auriga star-forming region has a very high fraction of binaries for G stars and probably even for M stars. This produced a thought that most stars might be forming as multiples, but later these systems are broken apart.
High-mass vs. low-mass stars and the multiplet frequency
Low-mass star systems are observed to have a much lower binary fraction than higher mass stars (Lada 2006). In the recent simulations of a turbulent molecular cloud destined to form a small cluster of low-mass stars several classes of systems were produced: isolated stars, binaries and multiples formed via the fragmentation of a turbulent core, and binaries and multiples formed via the fragmentation of a disk; however, dynamical filament fragmentation is the dominant mechanism forming low-mass stars and binary systems, rather than disk fragmentation. (Offner et al. 2010). Loosely bound companions can be stripped by close encounters within the protocluster. Although previous studies suggested that multiple star formation via the fragmentation of a disk was limited to large mass ratio systems, recent work such as Stamatellos & Whitworth (2009) and Kratter et al. (2010a) has shown that when disks continue to be fed at their outer edges, the companions can grow substantially. Protostellar disks that are sufficiently massive and extended to fragment might be an important site for forming brown dwarfs and planetary mass objects (Stamatellos et al. 2011). Cores that form brown dwarfs would have to be very small and very dense to be bound (Offner et al. 2008).
Protostellar cores with a mass of a few tenths to a few hundreds of solar appear to be more turbulent, with gas within generally moving at higher velocities. Those are more prone to fragmentation, giving birth to binaries or multiple stars. Such massive star forming sites are rare and thus tend to be farther from Earth (> 400 pc) than low-mass star forming regions (around 100 pc). High-mass star formation occurs in clusters with high stellar densities. In addition, massive stars destroy their natal environment via HII regions. Their accretion disks are deeply embedded in dusty envelopes and ultra-compact HII regions become visible only after star formation is nearly complete. Observations of HII regions produced by massive stars are a prime tool for extragalactic astronomers to determine the star formation rate and abundances in galaxies.
Massive stars are shorter-lived and interact more energetically with their surrounding environment than their low-mass counterparts; they reach main sequence faster and begin nuclear burning while still embedded within and accreting from the circumstellar envelope. They also can be potential hazards to planetary formation: many low-mass stars are born in clusters containing massive stars whose UV radiation can destroy protoplanetary disks.
The temperature structure of the collapsing gas strongly affects the fragmentation of star-forming interstellar clouds and the resulting stellar initial mass function (IMF). Radiation feedback from embedded stars plays an important role in determining the IMF, since it can modify the outcome as the collapse proceeds (Krumholz et al. 2010). Radiation removes energy, allowing a collapsing cloud to maintain a nearly constant, low temperature as its density and gravitational binding energy rise by many orders of magnitude. Radiative transfer processes can be roughly broken into three categories: thermal feedback, in which collapsing gas and stars heat the gas and thereby change its pressure; force feedback, in which radiation exerts forces on the gas that alter its motion; and chemical feedback, in which radiation changes the chemical state of the gas (e.g. by ionizing it), and this chemical change affects the dynamics (Krumholz 2010).

In this image surface column densities L= 0.1, M=1.0, H=10.0 g cm-2 are shown. As density increases, the suppression of fragmentation increases: (L) small cluster, no massive stars, depleted disks; (M) massive binary with 2 circumstellar disks and large circumbinary disk; (H) single large disk with single massive star.
The effects of radiative heating depend strongly on the surface density of the collapsing clouds, which determines effectiveness of trapping radiation and accretion luminosities of forming stars. Surface density is also an important factor in binary and multiple star formation. Higher surface density clouds have higher accretion rates and exhibit enhanced radiative heating feedback, diminished disk fragmentation and host more massive primary stars with less massive companions (Cunningham et al. 2011).
Observations indicate most massive O-stars have one or more companions; binaries are common (> 59%) (Gies 2008). Massive protostellar disks are unstable to fragmentation at R ≥ 150AU for a star mass of 4 or more solar masses (Kratter & Matzner 2006) and cores with masses above 20 solar will form a multiple through disk fragmentation (Kratter & Matzner 2007). Radiation pressure does not limit stellar masses, but the instabilities that allow accretion to continue lead to small multiple systems (Krumholz et al. 2009).
The upper limit on the final companion star frequency in the system can be estimated (Bate 2004).
Primordial stars and their legacy
The similar pattern appears in formation of previously believed to be solitary primordial stars. Recent studies suggest that loners were rather an exception, than the rule.
First massive stars were probably accompanied by smaller stars, more similar to our Sun. Due to encounters with their neighbors some of the small stars may have been ejected from their birth group before they had grown into massive stars. This could indicate primordial stars with a broad range of masses: short-lived, high mass stars capable of enriching the cosmic gas with the first heavy chemical elements and produced first black holes that are alive and well today, and long-lived, low-mass stars which could survive for billions of years and maybe even to the present day.
Are single stars really single?
Again, similar fragmentation happens in the massive protoplanetary discs to produce gas giants, when a gas patch in protoplanetary disk collapses directly into gas giant planet (1 Jupiter mass or larger) due to gravitational instability. Gravitational instabilities can occur in any region of a gas disk that becomes sufficiently cool or develops a high enough surface density, be it a star or a planet formation site. Kratter et al. 2009 suggests that planets formed that way might be failed binaries.
In 1970 Stephen Dole performed planet accretion simulation which produced interesting results. In our Galaxy, the average separation of binary components is about 20 AU, corresponding roughly to the orbital distances of the jupiter-mass gas giants in our solar system (Jupiter and Saturn have often been called “failed stars”; however, both probably contain rocky cores, so they are definitely planets). By increasing the density of the initial protocloud an order of magnitude higher than before, Dole’s program generated larger and larger jovians. Eventually in one high-density run, a class K6 orange dwarf star appears near Saturn’s present orbit, along with two superjupiters and a faint red dwarf further sunward. No terrestrials were formed.
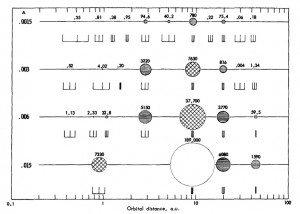
This study suggested that Jovians (brown dwarfs can be mentioned here too now) multiply at the expense of terrestrials. An increase of one critical parameter – the nebular density – resulted in the generation of binary and multiple star systems, and close companionship might lead to eventual exclusion of terrestrial worlds.
But things appear to be more complicated.
Terrestrial planets in multiple star systems
Multiple star systems provide a complicated mix of conditions for planet formation, because the accretion potentially involves material around each star in addition to material around the group. These locations can provide opportunities as well as hazards.
Binary systems can have circumprimary (around the more massive star), circumsecondary (around the less massive star), and circumbinary (around both stars) disks, compared to likely routine planet formation sites around single stars. In widely spaced binaries you could even have protoplanetary discs around the two.
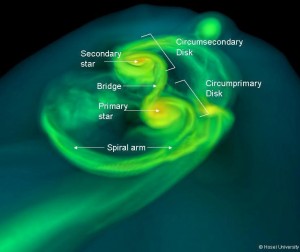
If there are no tidal effects, no perturbation from other forces, and no transfer of mass from one star to the other, a binary system is stable, and both stars will trace out an elliptical orbit around the center of mass of the system.
A multiple star system is more complex than a binary and may exhibit chaotic behavior. Many configurations of small groups of stars are found to be unstable, as eventually one star will approach another closely and be accelerated so much that it will escape from the system. This instability can be avoided if the system is hierarchical. In a hierarchical system, the stars in the system can be divided into two smaller groups, each of which traverses a larger orbit around the system’s center of mass. Each of these smaller groups must also be hierarchical, which means that they must be divided into smaller subgroups which themselves are hierarchical, and so on.
For a certain range of stellar separations, the presence of a companion star will clearly impact the formation, structure, and evolution of circumstellar disks and any potential planet formation. Global properties such as initial molecular cloud angular momentum, stellar density, the presence of ionizing sources and/or high mass, and so on, may all influence disk and thereby planet formation.
The maximum separation of bound systems is related to the stellar density. The denser clusters, in which most stars form, contain a lower fraction of bound multiple systems, comparable to the fraction found among field stars.
The binary star systems that host planets are very diverse in their properties and binary binary semimajor axes ranging from 20 AU to 6400 AU. In case where orbits are eccentric, the binary periastron can be as small as 12 AU, and important dynamical effects are expected to have occurred during and after planet formation.
In a circumbinary disk strong tidal interactions between the binary and disk are almost always expected, significantly affecting planet formation.
In a circumstellar disk with separations of a few to several tens of AU, the tidal torques of the companion star generate strong spiral shocks, and angular momentum is transferred to the binary orbit. This in turn leads to disk truncation, determining a “planet-free” zone (at least for formation). Subsequent dynamical evolution in multiple systems could still bring planets into this region.
For a circumstellar disk in a binary system, which is not influenced by strong tidal forcing, the effect of the companion star will be modest, unless the orbital inclinations are such that the Kozai effect becomes important.
Math Box 1 – The Truncation Radius
The truncation radius rt of the disk depends on the binary semimajor axis ab, its eccentricity eb, the mass ratio q = M2/M1 (M1, M2 denote the masses of the primary and secondary stars, respectively), and the viscosity v of the disk. For typical values of q = 0.5, eb = 0.3 and disk Reynold’s number of 10^5, the disk will be truncated to a radius of rt = 1/3ab.
For a given mass ratio q and semimajor axis ab an increase in eb will reduce the size of the disk while a large v will increase the disk’s radius. Not only will the disk be truncated, but the overall structure and density stratification may be modified by the binary companion.
In a circumbinary disk, the binary creates a tidally-induced inner cavity. For typical disk and binary parameters (e.g., eb = 0.3, q = 0.5) the size of the cavity is = 2.7 * ab.
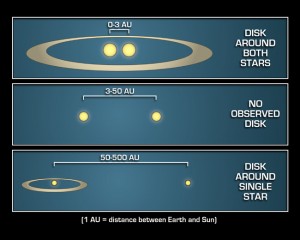
Numerical studies of the final stages of terrestrial planet formation in rather close binaries with separations of only 20–30 AU, that involve giant impacts between lunar-mass planetary embryos, show that terrestrial planet formation in such systems is possible, if there was a possibility for planetary embryos to form.
Systems with higher eccentricity or lower binary separation are more critical for planetesimal accretion. The effects of such eccentric companion include planetesimal breakage and fragmentation because of the increased relative velocities; the circumprimary planet forming disc truncation to smaller radii, causing the removal of material that may be used in the formation of terrestrial planets; destabilization of the regions where the building blocks for these objects may exist.
For binaries with separation less than 40 AU, only very low eccentricities allow planetesimal accretion to proceed as in the standard single-star case. On the contrary, only relatively high eccentricities (at least 0.2 in the closest 10AU separation and at least 0.7 for star system semimajor at 40AU) lead to a complete stop of planetesimal accretion.
A binary companion at 10 AU limits the number of terrestrial planets and the extent of the terrestrial planet region around one member of a binary star system.
Larger periastra (> 20AU) in solar-type binary star systems with terrestrial planets formation allow the stability of Jovian planets near 5 AU. These binary star/giant planets systems effectively support volatile delivery to the inner terrestrial region.
Approximately 40–50% of binaries are wide enough to support both the formation and the long-term stability of Earth-like planets in orbits around one of the stars. Approximately 10% of main sequence binaries are close enough to allow the formation and long-term stability of terrestrial planets in circumbinary orbits. According to this, a large number of systems can be habitable, given that the galaxy contains more than 100 billion star systems, and that roughly half remain viable for the formation and maintenance of Earth-like planets.
Math Box 2 –
Stability of the satellite-type orbit, where the planet moves around one stellar component (S-Type Orbits).In this equation, ac, the critical semimajor axis, is the upper limit of the semimajor axis of a stable S-type orbit, ab and eb are the semimajor axis and eccentricity of the binary, and mu = M2/(M1+M2). S-type orbits in binaries with larger secondary stars on high eccentricities are less stable. The +- signs define a lower and an upper value for the critical semimajor axis which correspond to a transitional region that consists of a mix of stable and unstable orbits.
Stability of the planet-type orbit, where the planet surrounds both stars in a distant orbit (P-Type Orbits).
For circular binaries, this distance is approximately twice the separation of the binary, and for eccentric binaries (with eccentricities up to 0.7) the stable region extends to four time the binary separation. A critical semimajor axis below which the orbit of the planet will be unstable is given by
Similar to S-type orbits, the +- signs define a lower and an upper value for the critical semimajor axis ac, and set a transitional region that consists of a mix of stable and unstable orbits.
Habitable zones in binary star systems
HZs in binaries depend the binaries’ orbital elements and the actual amount of radiation arriving at an orbiting planet. The analytical estimate on the extent of the HZs includes the radiation field of the binary as a function of spectral types, orbital parameters, as well as the relative orbital phase and calculations of the RMS (root-mean-square) and Min-Max distances of the inner and outer borders of the habzones in P-Type and S-Type configurations.
In a binary-planetary system, the presence of the giant planet enhances destabilizing effect of the secondary star. The Jovian planet perturbs the motion of embryos and strengthens their radial mixing and the rate of their collisions by transferring angular momentum from the secondary star to these objects.
Systems with close-in giant planets may require massive protoplanetary disks to ensure that while planetesimals and protoplanets are scattered as giant planets migrate, terrestrial bodies can form and be stable. Systems with multiple giants also present a great challenge to terrestrial planet formation since the orbital architectures of such systems may limit the regions of the stability of smaller objects.
Four different types of orbits are possible for a terrestrial planet in a binary system that hosts a Jovian planet: the terrestrial planet is inside the orbit of the giant planet; the terrestrial planet is outside the orbit of the giant planet; the terrestrial planet is a Trojan of the primary (or secondary) or the giant planet; the terrestrial planet is a satellite of the giant planet.
When numerically studying the dynamics of a terrestrial planet in a binary planetary system, integrations have to be carried out for a vast parameter-space. These parameters include the eccentricities, semimajor axes, and inclinations of the binary and the two planets, the mass-ratio of the binary, and the ratio of the mass of the giant planet to that of its host star. The angular variables of the orbits of the two planets also add to these parameters.
Except for a few special cases, the complexities of these systems do not allow analytical solutions of their dynamics, and require extensive numerical integrations. Those special cases are: binaries with semimajor axes larger then 100 AU in which the secondary star is so far away from the planet-hosting star that its perturbative effect can be neglected; binaries in which the giant planet has an orbit with a very small eccentricity (almost circular); binaries in which, compared to the masses of the other bodies, the mass of the terrestrial planet is negligible.
Instability is not the only hazard in multiple systems. The difference in masses and lifetimes can pose serious problems for life, especially in relatively close binaries or multiples.
Binary or multiple systems might be hosts to several generations of planets; life might arise and be wiped out several times in system’s lifetime. Here’s how such binary system might evolve: while both stars are on the main sequence and in close proximity to each other, small and close-in first generation of planets forms; eventually one star evolves from the main sequence into the red giant and the two stars spread further apart while stellar material blown off from the red giant builds a protoplanetary disk around the other star and second generation planets form; the second star eventually goes red giant giving the first star, which is now white dwarf, a protoplanetary disk which could create a third generation of planets.
Each generation of planets is built from stellar material with a sequentially increasing metallicity as the material is recycled within each star’s fusion processes. In this case it becomes possible for old stars, even those which formed as low metal binaries, to develop rocky planets later in their lifetimes.
However, not always changing environment might be a threat, like in case of this old gas giant PSR B1620-26 b.
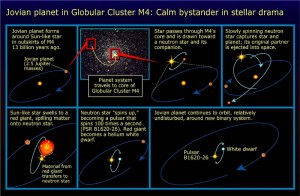
If such planet hosted habitable satellites, and host stars remained warm and safe enough to support life, inhabitants might not been affected much by dramatic changes. Or maybe they would. But that is another story.
# Pretty much everything in this article is presently under active research. To learn more about multiple star systems and habitable planets in them, try Planets in Binary Star Systems by Nader Haghighipour, 2010; or Multiple Stars across the H-R Diagram (you can read it online), 2005.
## Have fun and more exciting stuff to follow.

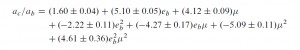
Do you have a source to reference for the critical orbit equations?
More importantly, to me, in the case of P-type orbits, is µ simply the sum of the stellar masses or is it also M2/(M1 + M2))? In the case of the latter, which star is considered M2 vs. M1?
µ = M2/(M1 + M2) and M1, M2 denote the masses of the primary and secondary stars, respectively.
As for the source, it was a book. I don’t remember which one, I would need to check. It’s been 2011..
Heh. My google-fu was with me for a change. A bit of searching found me “On the stability of S and P type orbits”(De Cesare and Capuzzo-Dolcetta, 2015) here
http://www.astro.lu.se/lundexoplanets2015/slides/Giovanni_de_Cesare.pdf
There I found the formula you reference on page 11. This had a reference to “LONG-TERM STABILITY OF PLANETS IN BINARY SYSTEMS”(Holmann and Wiegert, 1999), here
http://iopscience.iop.org/article/10.1086/300695/pdf
The important bit, for me, was this,”By the mass ratio µ = m2/(m1 + m2) is meant, where m1 is the mass of the star the test particle is orbiting and m2 is the mass of the per- turbing star.” That’s important, because it means I get different results for S-type systems orbiting each star. It also says this about P-type systems, “…only the range 0.1 ≤ µ ≤ 0.5 has been studied in the outer region, since systems with mass ratios of µ and 1 – µ are equivalent in this regime (with the exception of a 180º change in the particles’ longitudes)…,” which, while logically appropriate, isn’t true of the formula. For this, I will strictly use m1 as the larger body and m2 as the smaller. That should work.
This probably took inordinately long for me to figure out, but I figure the references might be welcome.
My recent blog post: Interlude: tectonics.js
The formulas in my article are given as ratios — they come from another place. It is mentioned at the end of the article…
https://books.google.lv/books?id=kyf7vgv6FSYC&pg=PA284&lpg=PA284&dq=Planets+in+Binary+Star+Systems+by+Nader+Haghighipour,+2010&source=bl&ots=5hTkAqikVB&sig=9O6YUiuqcG0o44kRJZ5VjZIUITE&hl=en&sa=X&ved=0ahUKEwib2Lyi2c3MAhVmG5oKHcorCacQ6AEIMzAE#v=onepage&q=Planets%20in%20Binary%20Star%20Systems%20by%20Nader%20Haghighipour%2C%202010&f=false