This post is for those, who will be modeling their planet atmospheres in detail. If you have used Starform (accrete) code to generate your system and evolved the system with Mercury afterwards, using a climate model for your planet would be a good choice to continue.
Before I will go into details with data preparation and actual modeling, there are multiple issues with compiling some parts of the FORTRAN code, especially the ones containing f90 or fIV/f66 features. For *nix systems ifort and f90 compilers are the necessary choice.
Now, I know for sure f77, gfortran, g95 or FTN95 won’t be much help. (The latter is Windows only; now with this one I’m not exactly sure, but I couldn’t make it compile with 8 byte-integer AND real options, it allowed me one or another, and not both; even if it is possible, it is NOT OBVIOUS HOW at all.) For Windows users issues are resolved with Compaq Visual FORTRAN Professional v6.6, for example, or Intel’s ifort compiler if you have one. I like Compaq better because you don’t need to install Visual Studio additionally, and it handles pretty much everything. Please note that version 6.5 or lower won’t do because of the integer/real intrinsic data types support (8 bytes are necessary).
Once you are technically set, you can move onto the next phase of atmosphere/climate modeling – data preparation. It is also assumed that you have decided on the atmospheric composition. I’m not an astrophysicist, so everything I do below this point is what I have came up so far by guess, trial and error method (yes, I’m THAT persistent) and is not claimed to be flawless.
Comments, suggestions and corrections are welcome.
Data preparation
I’ll start with the 1-D coupled model and there are several things to do before actual modeling.
Stellar spectrum. If you are using BaSeL server, your output is the flux moment given in erg/cm^2/s/Hz/sr. To get this in ergs/s/cm^2/Hz you need to multiply it by PI to get rid of steradians (sr). Then, flux Flambda, in units ergs/s/cm^2/Angstrom, can be calculated using the equation Flambda=0.4*flux_moment*c/Lambda^2, where c=2.997925e17 is the velocity of light and Lambda is the wavelength in nanometers. The numerical factor of 0.4 (=4*0.1) in equation above comes from the conversion of the flux moment into flux (*4) and from the conversion of flux per nanometer into flux per Angstrom (*0.1). However Flambda still is a flux at the surface of a star.
The flux at the top of the atmosphere is used in models; the altitude of 100 km is taken as „the top”. For Earth, an altitude of 120 km marks the boundary where atmospheric effects become noticeable during spacecraft re-entry. Most of the atmosphere (99.9999 percent) is below 100 km, although in the rarefied region above this there are auroras and other atmospheric effects.
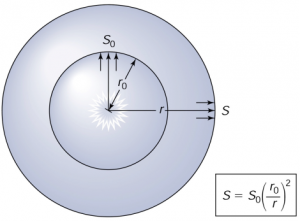
Now, flux, S, from a star drops off with increasing distance. In fact, it decreases with the square of the radial distance, r, from the star, as proportional to 1/r^2. You will need to provide distance in parsecs (see Stellar distance d in pc below).
There is also an option to obtain stellar spectrum by using ATLAS9 (or ATLAS12) and SYNTHE programs by Kurucz and Castelli (or SPECTRUM by Richard O. Gray, needs Atlas or MARCS stellar atmosphere model anyway). Here you can be more detailed with your star, providing additional initial conditions like microturbulent velocity* and mixing length parameter** into model. Then, there is also Chris Sneden’s MOOG.
*Microtubulent velocity. This is one of the fundamental stellar properties, a standard parameter in one-dimensional analyses of solar-type stars. For ATLAS models the value of microturbulent velocity, ξ, can be chosen [among 0, 1, 2, 4, etc. km/s] appropriate for the star’s surface gravity between the two velocities that bracket the microturbulent velocity. HOWEVER, the relation given by Kirby (Eq. 2 of Kirby et al. 2009, also here): ξ (km/s) = (2.13 ± 0.05) − (0.23 ± 0.03)*log g is only appropriate for giants, not sub-giants or dwarfs. Of course, for dwarfs there also exists a correlation between the luminosity class and the surface gravity (log g), the microturbulent velocity (t), and the metallicity ([M/H]) (Gray et al, 2000).
Dwarfs (V class) from F to G have the smallest microturbulent velocity, thus, technically, the higher the log g, the lower the microturbulent velocity. For precise results the technique of partial correlation can be employed, since the relationships between three or more random variables are being investigated. The trends for K stars (at least up to mid-K) are probably mainly similar to G dwarfs (Spectral studies of K dwarfs, Spectroscopic Properties of Cool Stars).
**Mixing length (ML) parameter. It is the alpha (a = l/Hp) parameter used in stellar model, which represents the ratio between the mean free path of a convective element (l) and the pressure scale height (Hp). The variations of this parameter strongly affect the structure of the outer envelope (i.e. radius and temperature). In fact, this parameter determines the efficiency of energy transport by convection in the outermost layer of a star: for a given stellar luminosity, it fixes the radius of the star, hence its temperature and color. In case of a real star, evolutionary tracks must then be calibrated by comparison with stellar radii and/or temperatures derived from observations. The most obvious ML calibrator is the Sun. The ML parameter can be fixed by constraining theoretical solar models (i.e. with solar mass, age and chemical composition) to reproduce the solar radius. In low-mass stellar models the derived stellar radii depend on the opacity which significantly contributes in determining the temperature gradient in their turbulent external layers. Hence, stellar models, based on different opacity tables, could require different values of alpha. It means that a homogeneous dataset of stellar temperatures at different metallicities to properly calibrate the ML parameter is urgently needed before any further attempt to use evolutionary models to derive relevant properties of stellar populations (Ferraro et al. 2006).
Lyman alpha flux at the planet (xLy). Lyman-alpha line is the brightest emission line of neutral hydrogen at the wavelength of 1215.67 A (121.567 nm) in the spectrum (in some papers 1215.7 A or 1216 A is mentioned). Stellar Lya emission lines are important spectral features in the context of exoplanet stellar environment and stellar physics. The Lya line is used as a proxy for determining the temperature and pressure profiles of upper stellar atmospheres. Lya flux is extremely variable with time. To a first approximation the solar La flux is composed of a quiet and of an active component. The Sun’s active component changes with the 27 days period (1 rotation around its axis); the quiet one with the 11 year solar cycle. For the Sun, the integrated Lya line flux may change by 37% during one rotation and up to 50% over a couple of years.
These fluxes can be obtained from the catalogue; in case of a synthetic star Lyman-alpha flux is the flux integrated over the whole Lya emission line of the synthetic spectrum. The easier way around is to compute a synthetic stellar Lya profile of a given linewidth, applying a simple linear rescaling in wavelength to the solar Lya profile. Real stellar profiles may be poorly represented by such a simple rescaling of the solar profile.
Math Box 1 – Some interesting data about your star
If you made yourself a synthetic star, some things are not given, but can be obtained through calculation. Now I was thinking if I need to include this in one of my posts, but heck, maybe it can be useful to someone.
If you know B-V color (from synthetic spectrum or from stellar data), then use it. Otherwise it can be calculated as B-V = (-3.684*LOG(Teff,K))+14.555. You can compare this data with the one from BaSeL result, for example, and make necessary adjustments.
Stellar rotation (vsin i)
Now, this one is tied to B-V and stellar age. I picked up formulas from (Barnes, 2007). Gyrochronology permits the derivation of ages for solar- and late-type main sequence stars using only their rotation periods and colors. If you know the age of your star and B-V color, you can go the other way around.
f(B-V) =0.7725*(((B-V)-0.4)^0.601), where B-V is the color;
g(t) = T^0.5119, where T is star age in Myr;
Rotational period P, days, is found as P = g(t)*f(B-V);
And finally, stellar equatorial rotational velocity, vsini, km/s, is found from the rotational period:
vsini = ((2*PI()*(R*2))/P)*(1/86400), where R is stellar radius and P is rotational period in days.
Stellar activity cycle
Approximate stellar cycle P, yrs, can be calculated as P = -1.22+(14.14*(B-V)). This is how long it takes your star to go from the minimum to maximum stellar activity. The complete cycle is, obviously, double of that.
Stellar distance d in pc. For your synthetic star you can take one of the provided distances (and manually scale the spectrum) for comparison with the VPL spectral data (I used 3.2 parsecs). If you used a real star, the real distance from Earth must be provided. It is needed for conversion to values expected for an Earth-like planet (see The Afac correction parameter). The flux will be scaled according to this distance.
The Afac correction parameter. To convert to values expected for an Earth-like planet, the measured UV fluxes were multiplied by ((206265*d )^2)*(Lsun/Lstar)*Afac, here d is the distance in parsecs (1 pc = 206264.806 =206205 AU), Lstar and Lsun are the respective bolometric luminosities of the star and the Sun, and Afac is a correction factor that accounts for the change in the planet’s albedo with the wavelength of the incident radiation. Values of Afac of 1.11 for the F2V star and 0.95 for the K2V star were obtained by scaling the “water loss” Seff limits in “Habitable Zones around Main Sequence Stars“, Kasting, J.F., Whitmire, D.P. & Reynolds, R.T. Icarus 101, 108-128 (1993), Table III, by the effective radiating temperature of the stars, using a quadratic fit to the listed temperatures. This procedure ensures that hypothetical planets would have the same surface temperature as the Earth (~288 K) if other climatic factors (e.g. cloudiness and greenhouse gas concentrations) are the same.
I went the other way around scaling given Afac numbers (x) to stellar temperatures (y):
| x | y | notes |
| 0.9 | 3450 | (M3.5V, AD Leo) |
| 0.95 | 5084 | (K2V, ε Eridani) |
| 1 | 5778 | (G2V, Sun) |
| 1.11 | 6930 | (F2V, σ Boo) |
Using quadratic regression I got coefficients for equation y=ax^2+bx+c:
a = -70906.1520; b = 158654.0223; c = -86698.5002
For any given temperature (K) within the range of [3450; 6930] you can solve the equation to find the roots:
x1 = (-b+SQRT((b^2)-4ac))/2a; x2 = (-b-SQRT((b^2)-4ac))/2a
Use the root that fits the range of Afac [0,9; 1,11] – in all cases here it will be x1.
Height of the tropopause. In planet.dat file you will need to provide the height of the tropopause. It is found to be strongly sensitive to the temperature at the planet’s surface through changes in the moisture distribution and its resulting radiative effects. The tropopause height is less sensitive to changes in the ozone distribution and hardly sensitive at all to moderate changes in the planet’s rotation rate (Thuburn & Craig, 1996).
Coupled photochemical and radiative/convective atmosphere model. When your data is ready, you can finally make executables and run your models. Make sure that everything in the files is set as you want it. And if you are running a coupled model, make sure your folder/file tree is put like it should be, and the couple switches in the code are on. Then, compile and run.
Some more alternatives
There is a very interesting model suite called Most for atmosphere and climate. It includes Planet Simulator, PUMA (The Portable University Model of the Atmosphere) and SAM (The Shallow Atmosphere Model) along with the Graphical User Interface, the Model Starter (MoSt), the postprocessor Burn7 and all manuals.
NOTE: There is no cake for Cygwin users here. You can get Most suite running under Cygwin (make sure X11 is properly set up), but the GUI is remarkably (read: awfully) slower than on Linux. Dual boot (Win/Linux) or “virtual machine” is the salvation.
Another model I’m going to mention here is called EPIC as in Explicit Planetary Isentropic-Coordinate general circulation atmospheric model. This model is implemented in principle for all known atmospheres (one for all!); for terrestrial-planet applications the EPICwiki suggests using version 4.x. (I would love to try this one once I have free time.)
# Have fun digesting and rejoice – there will be no more modeling for now (unless I’ll run into a proper planetary interior model. Yum.)
## Also, this is probably the last post this year but if you have questions or want to discuss something, feel free to drop a line. HAPPY WINTER HOLIDAYS and come back in January for more! 😉
